1991年高考，湖南、雲南、海南三省沒有使用全國統一的數學試卷，而是這三省共用一套試卷。本文就和大家分享一下當年三省數學試卷的壓軸題。

這道壓軸題放在現在難度並不算大，但是題目非常經典，30年後的現在仍然屬於常考題型，甚至高中數學學習中都會碰到類似的題目。接下來一起看一下這道題。

第一問證明函數的單調性，常用的方法有定義法和導數法。

證法一：定義法

定義法證明函數單調性可以歸結為5個步驟：取值、作差、變形、判號、下結論。

取值取的是引數的值，即x1、x2；作差做的是函數值之差，即f（x1）-f（x2）；變形是將函數值的差進行通分、提公因式、分子分母有理化等處理，最後變形幾個多項式的乘除的形式，方便判斷符號；判號就是判斷差的正負；下結論就是根據引數的大小及函數值的大小確定函數的單調性。

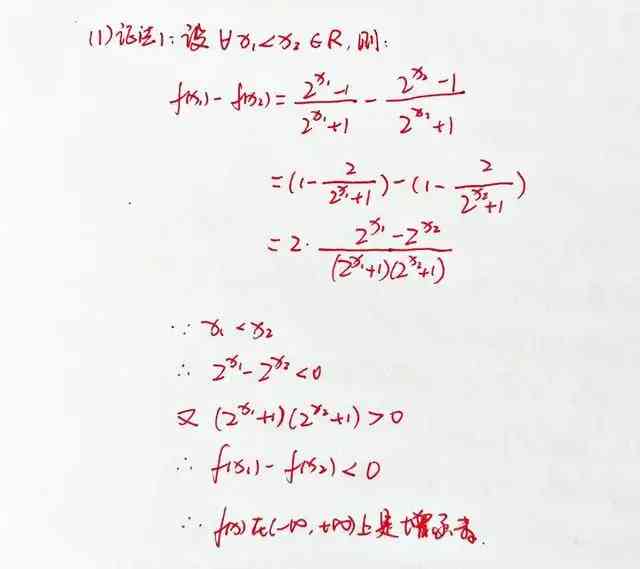
證法二：導數法

導數法證明函數單調性，先求導，再根據導數大於零函數為增函數，導數小於零函數為减函數來判斷。

本題中，對f（x）求導並化簡後可以得到：f'（x）=[2^（x+1）ln2]/（2^x+1）^2。

因為ln2＞0，2^（x+1）＞0，（2^x+1）^2＞0，所以f'（x）＞0，即函數為增函數。

如果本題是判斷函數單調性，那麼還可以利用函數單調性的一些常用性質快速判斷，但是要證明單調性最好還是用定義法和導數法。

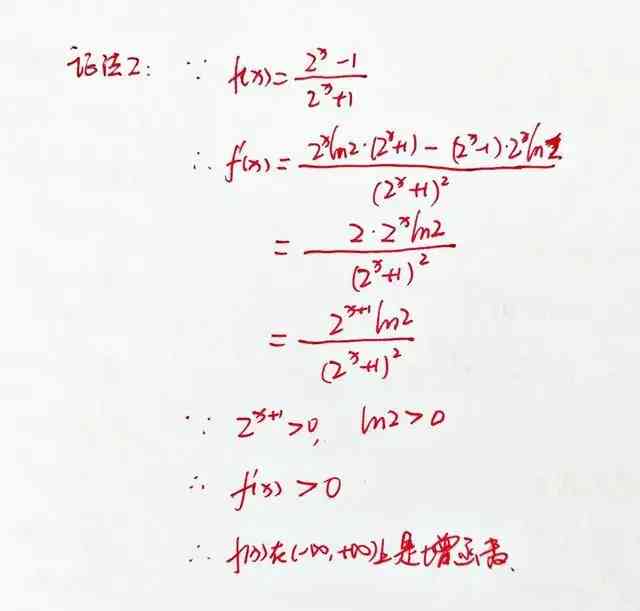
第二問證明不等式，先將f（x）的解析式代入後化簡，並只需證明當n≥3時2^n-1＞2n成立即可。本文介紹三種方法。

方法一：數學歸納法

當n=3時，上面的關係式成立。

假設當n=k（k≥3）時成立，則2^k-1＞2k，那麼當n=k+1時，2^（k+1）-1=2·2^k-1=2（2^k-1）+1＞2·2k+1=2（k+1）+2k-1。

又k≥3，所以2k-1＞0，即可證得當n=k+1時不等式依然成立。

方法二：導數法

先搆造函數g（x）=2^x-2x-1（x≥3），接下來只需要證明函數值恒大於零即可。

對g（x）求導，得到g'（x）=2^xln2-2。很明顯，g'（x）在x≥3上為增函數，所以g'（x）≥g'（3）=8ln2-2=2（ln16-1）＞0，所以g（x）為增函數。則有g（x）≥g（3）=2^3-2×3-1=1＞0，即g（x）＞0恒成立，從而證得結論。

方法三：組合數的性質

根據組合數的計算性質，將2^n寫成組合數的形式，然後兩邊同時减去1（Cn0），一邊就變成了2^n-1，另一邊就變成了2n再加上其他一些正數的形式，所以可以得到2^n-1＞2n。

本題的難度不大，但是屬於經典題目，特別是第一問現在仍然經常考試，需要特別注意。