親

愛的小夥伴們，微專題又和大家見面了，解題過程中，也許思緒萬千，也許毫無頭緒。如何就已有的思維和素養，步步分析，也許柳暗花明，直擊重點。今天我們以2021安徽中考壓軸為例，進行簡單的分析求解。

1

真題速遞

（2021·安徽）23.（本題滿分12分）如圖1，在四邊形ABCD中，∠ABC＝∠BCD中，點E在邊BC上，且AE//CD，DE//AB，作CF//AD交線段AE於點F，連接BF.

（1）求證：△ABF≌△EAD；

（2）如圖2，若AB＝9，CD＝5，∠ECF＝∠AED，求BE的長；

（3）如圖3，若BF的延長線經過AD的中點M，求BE:CE的值.

解析：由題幹易得，△ABE和△DCE都是等腰三角形，且相似。四邊形AFCD是平行四邊形。則AF=CD=DE，

（1）△ABF與△EAD中，

DE//AB，

∠BAF=∠AED，AF=DE，AB=AE，

則△ABF≌△EAD（SAS）.

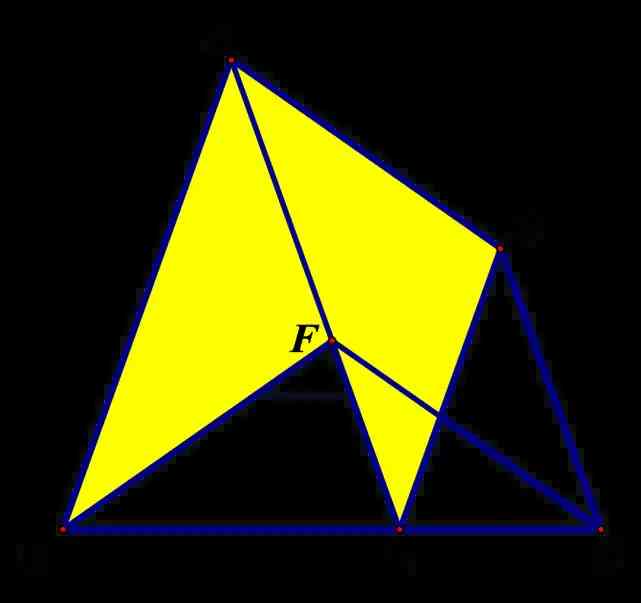
（2）由於（1）中沒有新增條件，所有（1）的結論可以在後面小問中直接應用，即BF=AD=CE，△FBC是等腰三角形。新增∠ECF＝∠AED，如圖所示四個角都相等，如何使用呢？

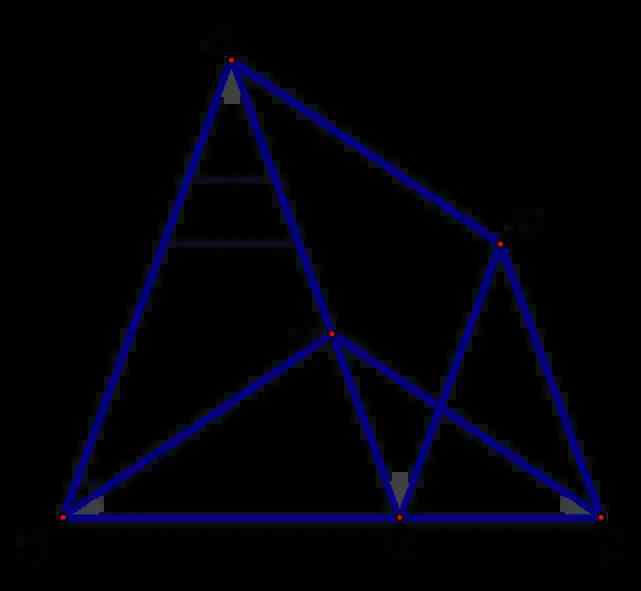
看題目所求，求BE的長，國中階段，求線段長，兩個辦法，相似與畢氏定理，本題與BE有關的線段直角特徵不明顯，且題中有很多相等的角，首先考慮相似。

再看已知，AB=9=AE，CD=DE=AF=5，還可以由EF=4.根據已知線段的特徵考慮BE，AE，EF有關線段構成的相似，易得，△ABE∽△BFE，這是一組共邊共角的子母型相似，根據比例式易得BE²=EF·AE=4×9=36，則BE=6.

（3）題目在前面已知的基礎上新增了一個條件，即M是AD中點。

關於中點的使用，在最近各位老師的解析裡面都考慮頗多，回頭看，題目所求，BE:CE，求一組線段的比，考慮轉化為其他線段的比，而本題沒有給出任何線段的長，只有M是中點所帶來的數量關係。怎麼辦呢？

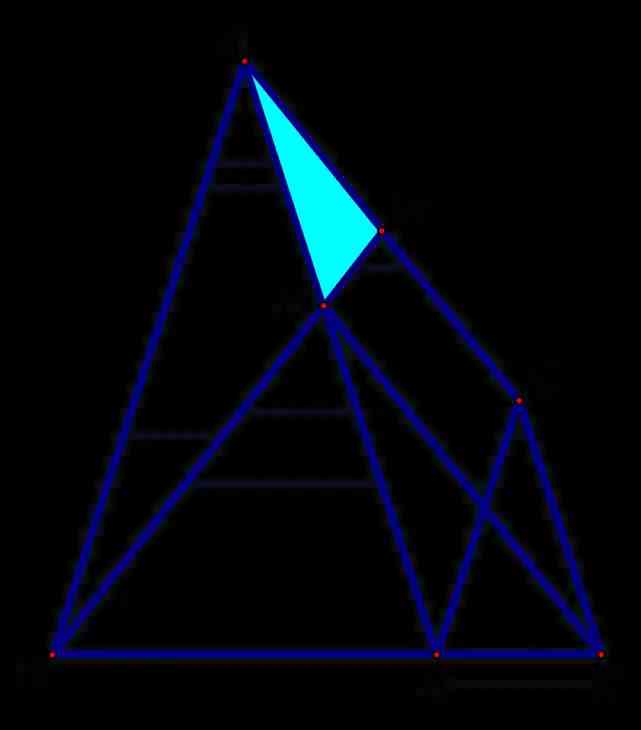
先看BE:CE可以如何轉化，根據題幹分析，△ABE與△DEC是相似的，

∴BE:CE=AB:DE，而AB=AE，DE=CD=AF，

再考慮AM與AD的數量關係，而AD=BF，所有的資訊都向一個地方靠攏，AM，AF，AB，BF，

一組相似浮現在眼前。

2

後記

回顧本道題，第一問全等的證明很簡單，但是很有用，在第二問，第三問都直接用到了全等的結論，邊相等和角相等。

本題設計巧妙，從圖形構成上來說，兩個等腰三角形的組合，如果共頂點，就是上期討論手拉手，本題時兩個底角共頂點，其實是另外一種圖形的構成策略（脚踢脚？），至於有什麼特殊的結論，大家不妨自行探索一下。

本題在解答過程中，不斷地根據已知，已證的結論，結合要求的結論，歸集方法，第（2）問，把要求的和已知結合在一起，問題集中在一組共頂點，共邊的相似三角形△ABE與△BFE中，同樣第（3）問，反思中點在最後求值的過程中的作用，歸結條件與結論，最後集中在△AMF與△BMA，得出一組比例式。此時各線段之間有一定的關係，但是不直接，借助設未知數的代數辦法，最後解方程，柳暗花明，瞬間明朗。

本題最後的難點突破在於借助代數方法設未知數，通過數與式的運算發現關係，從而得到結論，不失為一種好的探索方法，因為代數式的運算可以把線段之間關係直觀表現出來，直接進行加减乘除，山重水複疑無路，柳暗花明又一村。

本題第（3）問特殊的條件在於中點，大家可以圍繞中點再進行探索，本題還有一些的想法，如中點處倍長，如延長BA，CD相交於於P，則PE一定經過M等等結論。

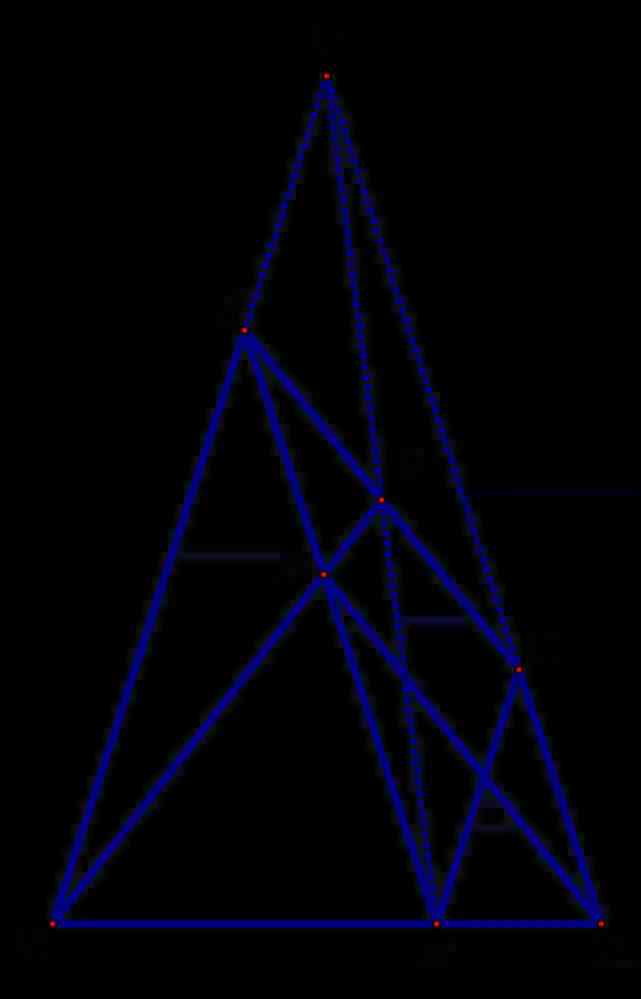
杭州陳漢老師利用此方法，一眼就構造出梅涅勞斯定理所需要的條件，

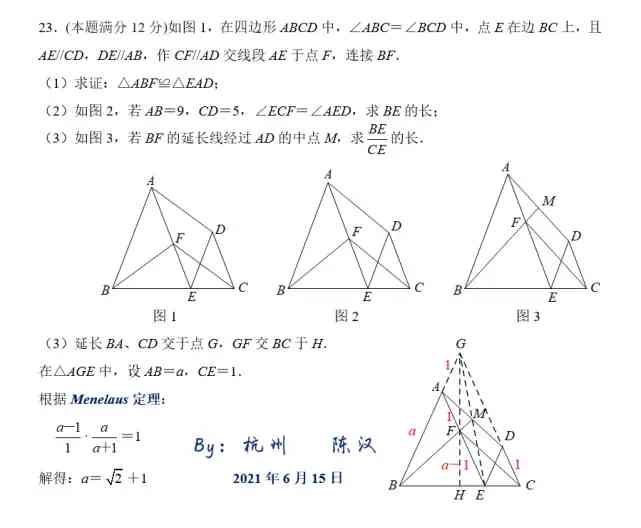
最後，關於本題，我們可以回望2013，安徽中考題

3

真題再現

（2013·安徽）23.我們把由不平行於底邊的直線截等腰三角形的兩腰所得的四邊形稱為“准等腰梯形”，如圖，四邊形ABCD即為“准等腰梯形”，其中∠B=∠C.

（1）在圖所示的“准等腰梯形”ABCD中，選擇合適的一個頂點引一條直線將四邊形ABCD分割成一個等腰梯形和一個三角形或分割成一個等腰三角形和一個梯形（畫出一種示意圖即可）；

（2）如圖，在“准等腰梯形”ABCD中，∠B=∠C，E為邊BC上一點，若AB‖DE，AE‖DC，求證：AB:DC=BE:EC.

（3）在由不平行於BC的直線AD截△PBC所得的四邊形ABCD中，∠BAD與∠ADC的平分線交於點E，若EB=EC，請問當點E在四邊形ABCD內部時（即圖所示情况），四邊形ABCD是不是“准等腰梯形”，為什麼？若點E不在四邊形ABCD內部時，情况又將如何？寫出你的結論.（不必說明理由）

熟悉不？大家試試吧？