注：此次推送不包括導數壓軸題，導數大題在後續的推送中專門給出。

浙江高考數學試卷的整體質量還是很高的，難度也高於新高考1卷，如果浙江省也使用新高考1卷，估計浙江的學子能樂醒，此次就不全盤分析了，選取幾道有思考價值的題目做一次分享。

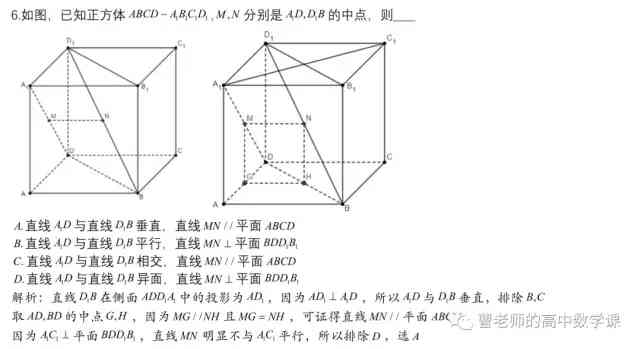
很明顯能看出兩直線异面且不平行，排除B，C，線段MN在底面ABCD上的投影為GH，在平行四邊形中證明線面平行即可，在正方體中與BDD1B1垂直的直線為AC，AC和MN顯然不平行，故MN不可能與平面BDD1B1垂直。

根據兩函數和目標函數的奇偶性對比，可排除A，B，從影像可知，當x趨近於正無窮時，y趨近於0，g（x）為有界函數，當x趨近於正無窮時f（x）趨近於正無窮，所以y=g（x）/f（x）滿足要求，浙江學生對極限應該很熟悉了，至於C選項的排除，可用導函數在π/4時的正負來判定。

這是一個很有意思的題目，如果能注意到給出的三個值中α，β，γ的正余弦正好全部出現，那麼利用常用不等式可證得不可能同時取到大於二分之一的情况，其實題目能大致推斷出，以sinαcosβ為例，當兩個角度均為45°時乘積剛好為二分之一，所以α越接近直角，正弦越大，β越接近0°，余弦越大，確定出兩角大致的範圍即可判斷出三個值中肯定有一個不符合邏輯。

四個選項中均為直線，這點有點無言，如果題目設定為复选题或選項題會更好，因為ab>0，二次函數恒正或恒負，所以當等比數列為非零常數列時t=0，這裡就能推斷出軌跡的一種情况是直線，題目中判斷（s，t）的軌跡，即找到一個關於s，t的方程，此時與a，b無關，最好將a，b設為1，帶入三個函數求軌跡即可，難度不大。

以上解法僅供參考，還有其他簡單的解法，根式數列通項的求法，在之前有過一期推送，連結為一類根式型數列通項公式的求法，常用的方法為換元或配方，但本題目無論採用何種方法均不能把an的通項求出來，囙此題目應該是考查數列的放縮，將一個非常規數列放縮成常規數列，利用放縮可得到一個包含an的數列累加法的不等式，求出an的類通項公式（不等關係），再將原等式中分母中的根式去掉後可得到一個與an數列累乘法有關的不等式，即可求出關於an的左右不等式，求和判斷範圍即可。

數列放縮也是浙江模考和高考中常見的題型了，畢竟浙江高考非常喜歡出與數列不等關係有關的壓軸小題，曾經還以不動點的形式出現過，很值得研究。

設出點求出投影帶入後所求式子為二元二次的最小值，解决此類問題方法很多，基礎的可用主次元法，即分別將x，y看做未知數求兩次最值，高級一些的可用拉格朗日乘數法，連結為不等式專題之二元條件最值中的拉格朗日乘數法，也可使用權方和不等式法，另外本題可用幾何法求解，若將所求看做兩個距離，其中一個是動點（x，y）到原點的距離的平方，另外一個是動點（x，y）到直線x+2y-2=0的距離的平方，利用不等式，轉化為與兩個距離和有關的最小值，很顯然最小距離就是原點到直線的距離，這種方法很有意思。

由於填空題中出現了一個利用超幾何分佈求概率和期望的小題，此次大題中竟然沒有相關的大題，數列題難度不大，第一問常規的根據Sn和an的遞推公式求通項公式，第二問利用錯位相減法求出Tn，整理後的不等式可當做關於n的一次函數不等式，若不等式恒大於等於0，則保證斜率為正且n=1時函數值大於等於0即可，當然斜率為零時恰也符合。

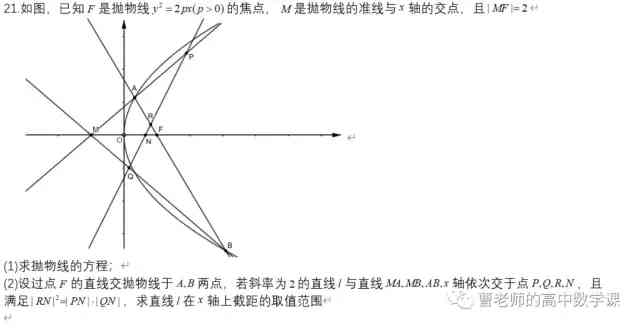
這個題目剛看到之後我都懷疑自己在規定時間內做不完，等式中的三段長度RN，PN，QN均為同一條直線上，且均以N為端點，N點恰好在x軸上，囙此等式可直接轉化為與R，P，Q三點縱坐標有關的等式，接下來表示出三個縱坐標即可。

因為抛物線焦點在x軸上，AB直線還過x軸上一定點，囙此設直線時把AB和l的方程設成x=my+n的形式會更簡單，聯立AB和l的方程可求出R點縱坐標，設出MA的方程與l聯立後可求出P點縱坐標，後可直接寫出Q點縱坐標，因為MA，MB的斜率形式類似，可設為k1，k2，先表示後帶入整理，整理之後發現過程並不複雜，化簡結果竟令人還有點小舒服，求最值需求一次最值，解一次不等式即可。

因為y1y2=-4，所以在化簡k1，k2時將分母中的4用-y1y1替換下來計算會更簡單，題目思路依舊很直觀，但咋一看的計算量確實嚇住很多人，實際上用時並不多，但如果一開始直線設成常規形式，4沒有用y1y2替換，那麼這個題目很大幾率是算不出來的。

關於最後一個導數題，浙江高考導數一向很奇怪，和全國1和新高考不是一個路子，所以非浙江省的人做起來會很不適應，就跟北京卷壓軸大題喜歡考類似於數論的題目一樣，做起來依舊不適應，不習慣，導數大題後期整理後專門給出。